必要十分条件の考え方は論理的思考の中で欠かせない。小学校で習う算数と中学以降に学ぶ数学の最も大きな違いは、算数では「十分」でよかったのが、数学では「必要」であることも求められるということなのではないかと思う。

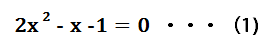
という数式があった場合に、xに当てはまる数を順番に考え、x=1 であればこの式が成り立つことを見出すのは算数的な考え方。確かにx=1はこの式を満たすが、数学ではx=1である必要があるか、というところまで考える必要がある。つまり、x=1ならば(1)が成り立つということだけでなく、(1)を成り立たせるためにはx=1であることが必要かどうかということも考えなければいけない。実際にはx=1であることは必要ではなく、x=-1/2という解も存在する。

算数の問題を解く小学生に限らず、日常生活で出会う種々の問題を解決しようとする人の多くは「できればいいじゃん」的な考え方で問題解決に当たっていることが多いと思う。実際、日常生活では、それが必要かどうかを考えなくてもよい場合が多い。たとえば、ある場所に行くためにすべての行き方を検討して、ベストな方法を検討する必要はない。ひとつ十分な解があればそれで事足りる。

しかし、場合によってはそれが必要かどうかということを改めて考えるとよりよい方法をみつけることができる。じゃがいもをゆでるのに水を温めてゆでればよいことを知っていても、ラップに包んで電子レンジで温める方がより簡単かもしれない。ガソリンを燃焼させることで車を動かせることを知っていても、電気で動かす方がより効率がよいかもしれない。じゃがいもをゆでるのに水を使うことや、車を動かすためにガソリンを燃焼させることは「十分」であっても「必要」ではない。何かアクションを取って、それがうまくいったとしても、それが「必要」なことだとは限らない。もっといい方法があったのかもしれない。過去の成功体験に囚われず、たまたま上手くいったのか、それともそれをやることが必要だったのか、検証することによって、次回、より適切なアクションを取ることができる。

ひとつの「十分」な解を知ってしまうと、ついついそれに頼ってしまいがちで、よりよい解を見つける気にはなかなかなれない。それはジャガイモのゆで方でも製品の開発でも同じこと。「できればいい」「動けばいい」というだけでなく、それが「必要」かということを考えることで、より適切な解を見つけられるかもしれない。